Por ejemplo la interseccion de un cono con un plano puede generar una parabola.
Para un modelador de mallas que se base en triangulos, no es nada trivial generar una malla a partir de 2 mallas originales y una operacion de interseccion o diferencia. Particularmente calcular la frontera entre los 2 objetos originales que se intersectan lleva a varias complicaciones, y la precision siempre es un problema. (*)
Afortundamente para un ray-tracer la GC es una operacion trivial, (o relativamente simple).
El caso de la interseccion A ^ B, si el rayo intersecta al objeto A en el pto Ip, solo hay que chequear que dicho pto pertenezca al volumen de B, y viceversa, si el rayo intersecta en el B, hay que chequear que el pto este en el interior de A.
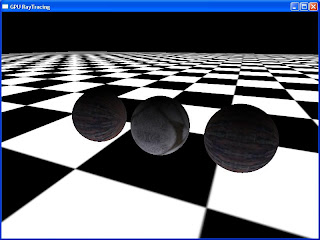
Ejemplo para la interseccion con 3 esferas:
// Geometria constructiva
// Objeto Interseccion M Interseccion M2
float4 M = tex2D( g_samObj2, float2(j+0.5,i+0.5)/OBJ_SIZE);
float4 M2 = tex2D( g_samObj3, float2(j+0.5,i+0.5)/OBJ_SIZE);
if(fl)
{
float3 pt = LF+D*t0;
float dist = distance(pt,float3(M.x,M.y,M.z));
// interseccion
if(dist>M.w)
fl = false;
else
{
dist = distance(pt,float3(M2.x,M2.y,M2.z));
if(dist>M2.w)
fl = false;
}
}
if(fl2)
{
float3 pt = LF+D*t1;
float dist = distance(pt,float3(M.x,M.y,M.z));
// interseccion
if(dist>M.w)
fl2 = false;
else
{
dist = distance(pt,float3(M2.x,M2.y,M2.z));
if(dist>M2.w)
fl2 = false;
}
}

El caso de la diferencia si A y B son 2 objetos el objeto A-B, se puede resolver en el tracing de la siguiente forma.
Supongamos que el rayo intersecto con el objeto A en el pto Ip, solo hay que chequear que Ip este incluido en el volumen de A. Si no llega a ser el caso, se anula esa interseccion rayo-A.
Usualmente A-B se completa agregando tambien B ^ A, para que dibuje el objeto entero.

Implementar la GC en forma general requiere hallar una formula o un metodo de determinar si un punto cualquiera esta o no dentro del volumen del objeto.
Para el caso de la esfera eso es trivial, y en general en el mismo momento que uno analiza las prop. geometricas de un cuerpo para hallar la formula de la interseccion con el rayo, con un poco mas de trabajo se puede llegar al calculo de inclusion del punto.
Si la formula analitica es muy dificil de hallar, siempre se puede calcular de la siguiente forma, si el cuerpo es "cerrado" e decir no tiene ningun agujero:
desde el pto en cuestion se traza un rayo hacia cualquier direccion, y se cuenta la cantidad de veces que intersecta sobre si mismo. Si esa cantidad es impar el punto estaba adentro del cuerpo. Justamente, la interseccion entre el rayo y el cuerpo ya la resuelta para el ray-tracing. (De lo contrario ese cuerpo no seria una primitiva de nuestro tracer)
Con lo cual implementar la GC en un ray-tracer es bastante directo.
(*) Hace unos años estaba implementando la Geometría Constructiva en el motor grafico que utilizo para mis sistemas, que esta basado en mallas. Internamente todos los objetos se convierten en una malla de triangulos, que luego se envian ahora a la GPU, antes al GDI del windows.
Generar la malla resultante fue sumamente dificil, y si bien a nivel grafico parecia funcionar bien, (siempre se puede ajustar el nivel de precision para que quede bien), a nivel analitico la frontera no quedaba perfectamente cerrada. Como la malla de salida se tenia que enviar en formato STL a una impresora 3d, el driver de la impresora no aceptaba huecos en la figura, asi como tapoco triangulos sueltos.
Programas como el Rhino que trabajan sobre Nurbs tienen implementado en su nucleo todas las operaciones de GC directamente sobre las curvas, y generan las mallas solo en el momento que se necesitan y con la precision requerida.
Ejemplo de un Toro menos otro toro, donde se ve que graficamente esta bien:

Sin embargo, de cerca la frontera, tiene huecos en algunos lugares. Ademas se ve como hay que empezar a tessellar los triangulos en la interseccion entre ambas figuras: