Las ecuaciones parametricas del toro de radio mayor R y radio menor r son:
x(u, v) = (R + r cos v) cos u
y(u, v) = (R + r cos v) sen u
z(u, v) = r sen v
Para una descripcion mas detallada del toru sus ecuaciones y propiedades:
http://es.wikipedia.org/wiki/Toro_(geometr%C3%ADa)
La interseccion entre el rayo y el toro requiere resolver la raiz de un polinomio de grado 4:
float AA = LF.x - toro.x;
float BB = LF.y - toro.y;
float CC = LF.z - toro.z;
float C = AA*AA+BB*BB+CC*CC-(toro_rx*toro_rx + toro_ry*toro_ry);
float B = 2*(D.x*AA+D.y*BB+D.z*CC);
float a2 = toro_rx*toro_rx;
float b2 = toro_ry*toro_ry;
// coefientes ecuacion cuarta
float r0 = 2*B;
float r1 = B*B + 2*C + 4*a2*D.z*D.z;
float r2 = 2*B*C + 8*a2*CC*D.z;
float r3 = C*C+ 4*a2*(CC*CC - b2);
entonces, la ecuacion que hay que resolver es
x^4 + r0 x^3 + r1 x^2 + r2 x + r3 = 0
Si metemos esto en un PS, nos queda asi:
// ecuaciones cuarticas
double solve_cubic(double a, double b, double c);
int solve_quartic(double a, double b, double c, double d, inout float results[4])
{
int num_roots = 0;
double a2 = a*a;
double k = a2 - 4*b;
double twice_y0 = solve_cubic(-b, a*c - 4*d,-k*d - c*c);
double alpha2 = k/4 + twice_y0;
if (alpha2 >=-EPSILON)
{
double alpha,beta;
double y0 = twice_y0/2;
if (abs(alpha2)<EPSILON)
{
alpha = 0.0;
beta = sqrt(y0*y0 - d);
}
else
{
alpha = sqrt(alpha2);
beta = (a*y0 - c)/(2*alpha);
}
double BB = a/2 - alpha;
double CC = y0 - beta;
double disc_sqr = BB*BB - 4*CC;
double disc;
if (abs(disc_sqr)<EPSILON)
{
results[0] = -BB / 2;
num_roots++;
}
else if (disc_sqr > 0)
{
disc = sqrt(disc_sqr);
results[0] = (-BB + disc)/2;
results[1] = (-BB - disc)/2;
num_roots+=2;
}
BB = a/2 + alpha;
CC = y0 + beta;
disc_sqr = BB*BB - 4*CC;
if (abs(disc_sqr)<EPSILON)
{
if(num_roots==0)
results[0] = -BB / 2;
else
if(num_roots==1)
results[1] = -BB / 2;
else
results[2] = -BB / 2;
num_roots++;
}
else if (disc_sqr > 0)
{
disc = sqrt(disc_sqr);
if(num_roots==0)
{
results[0] = (-BB + disc)/2;
results[1] = (-BB - disc)/2;
}
else
if(num_roots==1)
{
results[1] = (-BB + disc)/2;
results[2] = (-BB - disc)/2;
}
else
{
results[2] = (-BB + disc)/2;
results[3] = (-BB - disc)/2;
}
num_roots+=2;
}
}
return num_roots;
}
double solve_cubic(double a, double b, double c)
{
double Q = (a*a - 3*b)/9;
double R = (2*a*a*a - 9*a*b + 27*c)/54;
double Q3 = Q*Q*Q;
double disc = R*R - Q3;
double k2 = -a/3;
if (disc < -EPSILON)
{
// 3 raices reales
double theta = acos(R/sqrt(Q3));
double k1 = -2*sqrt(Q);
return k1*cos(theta/3) + k2;
//results[1] = k1*cos((theta + 2*M_PI)/3) + k2;
//results[2] = k1*cos((theta + 4*M_PI)/3) + k2;
//return 3;
}
else
{
// una raiz real
double disc2 = sqrt(disc) + abs(R);
double cuberoot = pow(disc2,1/3.0);
if (R < 0)
return (cuberoot + Q/cuberoot) + k2;
else
return -(cuberoot + Q/cuberoot) + k2;
}
}
void PS_RayTracing2( float4 Diffuse:COLOR0, float2 Tex : TEXCOORD0,
out float4 Color : COLOR0 )
{
// Calculo la direccion del rayo
float3 D = normalize(g_vViewDir + g_vDx*(2*Tex.x-1) + g_vDy*(1-2*Tex.y));
float R = 100000;
float3 Ip = 0;
float AA = LF.x - toro.x;
float BB = LF.y - toro.y;
float CC = LF.z - toro.z;
float C = AA*AA+BB*BB+CC*CC-(toro_rx*toro_rx + toro_ry*toro_ry);
float B = 2*(D.x*AA+D.y*BB+D.z*CC);
float a2 = toro_rx*toro_rx;
float b2 = toro_ry*toro_ry;
// coefientes ecuacion cuartica
float r0 = 2*B;
float r1 = B*B + 2*C + 4*a2*D.z*D.z;
float r2 = 2*B*C + 8*a2*CC*D.z;
float r3 = C*C+ 4*a2*(CC*CC - b2);
// Resuelvo la ecuacion cuartica
float roots[] = {0,0,0,0};
int cant = solve_quartic(r0,r1,r2,r3,roots);
if(cant>0)
Color.rgb = LF+D*roots[0]; // punto de interseccion
else
Color.rgb = 0;
Color.a = 1;
}
Desafortundamente, al correr este shader, comienzan a aparecer "huecos" por algunos lugares, en ciertos puntos donde por errores de redondeo o falta de precision, el algoritmo se vuelve numericamente inestable:

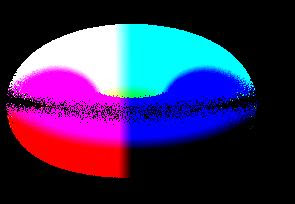
El algoritmo se hace mucho mas inestable en la medida que el toro se aleja o se alinea en ciertos angulos:

Como la solucion analitica sufre de problemas de estabilidad, probe de implementar una solucion numerica. El metodo de Laguerre para encontrar raices de polinomios tiene la ventaja de ser muy facil de implementar, y no requiere elegir un punto inicial especial (como el metodo dew Newton), con lo cual siempre converge (Se llaman metodos con convergencia Global, para distinguirlos del metodo de Newton que solo goza de convergencia Local)
http://en.wikipedia.org/wiki/Laguerre's_method
La implementacion en el PS:
double Laguerre(double x,double a, double b, double c, double d)
{
for(int k=0;k<20;++k)
{
double x2 = x*x;
double x3 = x2*x;
double x4 = x3*x;
double p0 = x4+a*x3+b*x2+c*x+d; // p(x)
if(abs(p0)<EPSILON) // ya encontre un raiz con suf. precision
k = 21;
else
{
double p1 = 4*x3+3*a*x2+2*b*x+c; // p'(x)
double p2 = 12*x2+6*a*x+2*b; // p''(x)
double G = p1/p0;
double H = G*G - p2/p0;
double disc = sqrt(abs(3*(4*H-G*G)));
double a = G>0?4/(G+disc):4/(G-disc);
x -= a;
}
}
return k>20?x:0;
}
Al correr el PS, se obtienen tambien puntos negros donde el rayo pierde la superficie del toro, con lo cual tampoco resulta numericamente estable:

Otra vez, la cantidad de pasos (ahora puesta en 20) es arbitraria, pero en este caso es muy dificil de encontrar un valor adecuado para todos los casos y que no sea demasiado alto para que no se haga tan lento.
Re-escribiendo las ecuaciones del toro, para que sea una funcion de 2 variables:
....
float d = R - sqrt(x*x + y*y);
float disc = r*r-d*d;
return sqrt(disc);
....
Con esta forma, podemos usar el metodo generico de avanzar sobre el rayo, en este caso solo vemos la parte de "arriba" del toro, que corresponde a la solucion positiva de la raiz.

No hay comentarios:
Publicar un comentario